ЗАДАНИЕ 24 ОГЭ МАТЕМАТИКА (ВАРИАНТ 164 АЛЕКС ЛАРИН)

Готовимся к ОГЭ по математике. Решаем задание 24 из второй части экзамена,  блок геометрия. Это задание из 164 варианта сайта alexlarin.net . Максимальное количество баллов, которое можно получить за задание составляет 2 балла, при условии что получен верный логически обоснованный ответ.

Задание 24 ОГЭ математика(вариант 164 Алекс Ларин)

Один из углов параллелограмма в 5 раз больше другого, а одна из его диагоналей является высотой. Найдите отношение диагоналей параллелограмма.

Дано: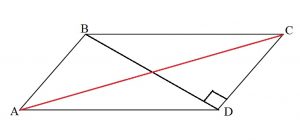    

ABCD — параллелограмм,

BD и AC — диагонали параллелограмма,

BD — высота,

один из углов параллелограмма в 5 раз больше другого.

_________________________________________

Найти: BD : AC.

Решение:

Определим какой из углов параллелограмма в 5 раз больше другого. По свойству параллелограмма имеем: противоположные углы параллелограмма равны. Значит, противоположные углы брать нельзя. Еще одно свойство параллелограмма гласит: сумма углов, прилежащих к одной стороне равна 180 градусам. Поэтому, рассмотрим углы А и В.

Пусть <A = x, тогда <B = 5x.

Составим уравнение: x + 5x = 180°, x = 30°.  <A =< С = 30°, <B = <D = 150°.

Рассмотрим ᐃBDC — прямоугольный, <D = 90°, <B = 60°, <С = 30°.

Воспользуемся формулами прямоугольного треугольника: катет лежащий напротив угла в 30 градусов равен половине гипотенузы. Обозначим BD = x, тогда BC = 2x.

По теореме Пифагора катет CD = √3x.  AB = CD = √3x, BC = AD = 2x (ABCD — параллелограмм).

Расcмотрим  ᐃACD и применим теорему косинусов к стороне AC, она же является диагональю параллелограмма ABCD.

AC² = AD² + CD² – 2AD·CD·cos150°,

AC² = 4x² + 3x² – 4x·√3x·cos150°,

AC² = 7x² + 4·√3x² ·√3:2,

AC² = 13x² ,

AС = √13x.

Найдем отношение диагоналей BD и AC параллелограмма ABCD.  BD : AC = x : √13x = 1:√13.

Ответ: BD : AC =  1:√13.

Рассмотрим еще одно задание по геометрии из 164 варианта только из первой части.

Задание 18  ОГЭ математика(вариант 164 Алекс Ларин)

В треугольнике ABC AC=3√7 , BC=3√2, угол C равен 90°. Найдите радиус окружности, описанной около этого треугольника.

Решение:

Радиус окружности, описанной около прямоугольного треугольника, равен половине гипотенузы. R = AB:2. Нам нужно найти гипотенузу

AB треугольника ABC по теореме Пифагора.

AB² = (3√7)² + (3√2)²  ,

AB² = 9·7 + 9·2,

AB² = 9(7 + 2),

AB² = 81,

AB= 9.

R=4,5.

Ответ: радиус окружности, описанной около треугольника, равен 4,5.