Задание 24 ОГЭ математика (Вариант 165 Алекс Ларин)

Готовимся экзамену  и подробно разбираем задание 24 ОГЭ математика из варианта 165 с сайта  alexlarin.net. Задание 24 находится во второй части экзаменационной работы. По критериям максимальная оценка за это задание составляет 2 балла, если полностью решена задача и получен верный обоснованный ответ. Если будет допущена вычислительная ошибка, которая приведет к неправильному ответу, при этом цепочка рассуждений верная, то задание будет оцениваться в 1 балл.

Задание 24 ОГЭ математика (Вариант 165 Алекс Ларин)

В прямоугольном треугольнике АВС из вершины прямого угла В проведены медиана ВЕ и высота ВК. Найдите длину гипотенузы АС, если КЕ = 1, <ВАК = 60°.

Дано: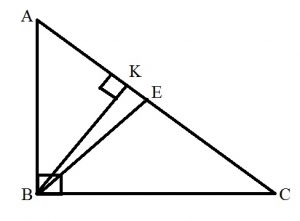                          

ᐃABC (<B = 90°),

BE — медиана,

BK — высота,

KE = 1,

<ВАК = 60°.

_______________

Найти: AC.

Решение:

1. Так как BE —  медиана — отрезок, соединяющий вершину с серединой противоположной стороны, то AE = CE. AC = AE + CE.
2. Применяем формулы прямоугольного треугольника: медиана, проведенная к гипотенузе прямоугольного треугольника, равна ее половине. BE = AC:2, BE = AE = CE.
3. Рассмотрим треугольник AEB. У него: BE = AE и  <ВАК = 60°. Поэтому, ᐃAEB — равносторонний и <BEA = 60°.
4. Рассмотрим треугольник BKE. Это прямоугольный треугольник, у которого  <KBE = 30°( сумма острых углов прямоугольного треугольника равна 90°). KE = BE :2 (катет, лежащий напротив угла в 30 градусов,равен половине гипотенузы), BE = KE · 2 = 1 ·2 = 2.
5. Имеем, BE = AE = CE = 2 и AC = AE + CE = 4.

Ответ: AC  = 4.

Рассмотрим еще одну задачу геометрического содержания из этого же источника. Эта задача по геометрии из первой части экзаменационной работы оценивается одним баллом.

Задание 19 ОГЭ математика (Вариант 165 Алекс Ларин)

Катеты прямоугольного треугольника равны 2√6 и 1. Найдите синус наименьшего угла этого треугольника.

Решение:

В прямоугольном треугольнике самый большой угол  — прямой, а напротив меньшего угла лежит меньшая сторона. Поэтому, наименьший угол этого треугольника будет лежать напротив меньшего катета, то есть равного 1. По определению синуса острого угла прямоугольного мы знаем, что это отношение противолежащего катета к гипотенузе. Нам нужно найти гипотенузу треугольника по теореме Пифагора( квадрат гипотенузы равен сумме квадратов катетов). Произведя несложные расчеты, имеем гипотенузу равную 5 . Далее находим синус наименьшего угла: 1: 5 = 0,2.

Ответ: 0,2.