Задание 13 Вариант 221 ЕГЭ профиль Алекс Ларин

Решаем тригонометрическое уравнение с выбором корней из промежутка. Это 13 тренировочное задание ЕГЭ профиль Алекс Ларин.

 Задание 13 Вариант 221 ЕГЭ профиль Алекс Ларин

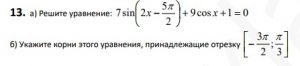
Решаем 1 часть 13-го задания. Преобразуем левую часть тригонометрического уравнения. Воспользуемся периодичностью функции синус, нечетностью синуса и формулами приведения.

-7cos2x + 9cosx + 1 =0.

Далее воспользуемся формулой косинуса двойного угла cos2x =2cos²x — 1.

-7(2cos²x — 1) + 9cosx + 1 =0,

-14cos²x  + 9cosx + 8 =0,

14cos²x  — 9cosx — 8 =0.

Введем замену cosx = t и получаем квадратное уравнение 14t²  — 9t — 8 =0.

D = 81 + 448 = 529>0(2 корня).

√D = 23.

x₁ = 32/28 и x₂ = -1/2.

Делаем обратную замену:

cosx = 32/28 (не подходит, так как |cosx| ≤1),

cosx = -1/2.

Изобразим решение этого уравнения на единичной окружности. Так как косинус —  это абсцисса, то через точку -1/2 проводим прямую параллельную оси Y. Эта прямая пересекает окружность в двух точках.

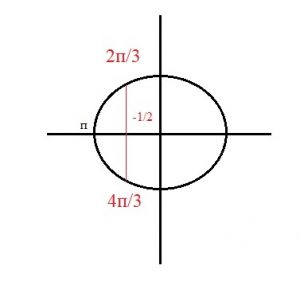
Запишем решения уравнения в общем виде.

x = 2π/3 + 2πn, x = 4π/3 + 2πn, n ∈ Z ( можно решения записать так — x = ±2π/3 + 2πn, n ∈ Z).

Решаем вторую часть задания 13 221  тренировочного варианта ЕГЭ  профиль.

Нам нужно выбрать корни из промежутка [3π/2; π/3].

Корни можно выбирать двумя способами:

1. с помощью тригонометрического круга;
2. с помощью нахождения целых n из решения неравенств.

Находим решения из промежутка вторым способом.

Решаем двойные неравенства относительно n.

3π/2 ≤2π/3 + 2πn≤ π/3,

3π/2 — 2π/3 ≤2π/3  — 2π/3 + 2πn≤ π/3 — 2π/3,

-13π/6 ≤ 2πn≤ -π/3 | : 2π,

-13/12 ≤ n≤ -1/6,

n = -1, x = 2π/3 — 2π = -4π/3.

3π/2 ≤4π/3 + 2πn≤ π/3,

-17/12 ≤ n≤ -1/2,

n = -1, x =4π/3 — 2π = -2π/3.

Ответ: а)  x = ±2π/3 + 2πn, n ∈ Z;  б) -4π/3; -2π/3.

Подробное решение задания 13 (вариант 15) из сборника для подготовки к ЕГЭ по математике профиль 2018 года, автор сборника Ященко И.В.