Разбираем профильный ЕГЭ по математике. Тренировочный вариант 222 Ларин решение задания 13. Это тригонометрическое уравнение с выбором корней из промежутка.
Задание 13 Вариант 222 Ларин решение
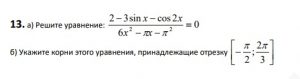
Найдем область определения уравнения. Уравнение имеет смысл, если знаменатель не обращается в нуль.
Приравняем знаменатель к нулю и решим квадратное уравнение.
6x2 -πx – π2 = 0,
Д = π2 +24π2 =25π2
Корни этого уравнения: -π/3 и π/2.
ОДЗ уравнения: x≠-π/3 и x≠ π/2.
Отбрасываем знаменатель и решаем уравнение
2 — 3sinx — cos2x = 0.
Сведем это уравнение к квадратному, преобразовав левую часть уравнения с использованием формулы косинуса двойного угла и основное тригонометрическое тождество.
2 — 3sinx — (cos2x – sin2x) = 0,
2 — 3sinx — (1 — sin2x – sin2x) = 0,
2sin2x — 3sinx +1 = 0.
Введем замену sinx = t, тогда уравнение примет вид 2t2 — 3t +1 = 0.
Корни этого уравнения имеют вид 1/2 и 1.
Делаем обратную замену.
sinx = 1,
x = π/2 + 2πn, n∈Z (n≠0)
sinx = 1/2,
x = π/6 + 2πk, k∈Z,
x = 5π/6 + 2πk, k∈Z.
Выбираем корни из указанного в задании промежутка.
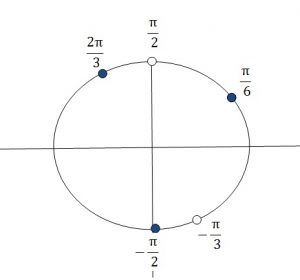
Из указанного промежутка подходит только корень π/6.
Ответ:
а) π/2 + 2πn, n∈Z (n≠0);
x = π/6 + 2πk, k∈Z;
x = 5π/6 + 2πk, k∈Z.
б) π/6.
