Колесо — это предмет, как правило, круглой формы, служащий для передачи или регулирования движения.
Кривые постоянной ширины
Использование колес для перемещения грузов по плоским поверхностям возможно благодаря тому, что все радиусы окружности имеют одинаковую длину. Так как окружность — это геометрическое место точек, равноудаленных от центра. Поэтому если ось вращения колеса проходит через его центр, то она не поднимается и не опускается, а только перемещается вперед или назад, при этом высота над поверхностью остается неизменной. Существует и другой способ перемещения грузов, в котором вместо колес используются валы. Все мы не раз видели на картинках, как огромный каменный блок стоит на нескольких валах и его толкают или тянут веревками
Это возможно благодаря еще одному свойству окружностей, которое не имеет ничего общего с тем, о чем мы только что говорили. Колеса могут иметь только круглую форму, в то время как форма валов может быть различной.
Свойство, благодаря которому действуют валы, связано не с расположением центра окружности, а с шириной круга, которая постоянна в любом направлении. Рассмотрим в качестве примера эллипс. Ширина эллипса вдоль большой оси очевидно больше, чем вдоль малой оси. Нетрудно представить, что произойдет, если мы подложим под камень валы в форме эллипса.
Камень при движении будет перемещаться вверх-вниз, пока не упадет на землю. Любопытно, но окружность не единственная кривая постоянной ширины. Существует бесконечное множество подобных прямых, которые подчас имеют весьма причудливую форму
Как построить треугольник Рёло
Пусть дан равносторонний треугольник с вершинами А, В и С. Возьмем циркуль и проведем дугу окружности с центром в точке А через вершины В и С. Затем проведем дугу окружности с центром в точке В. Дуга пройдет через вершины С и А. После этого выполним аналогичные действия для вершины С.
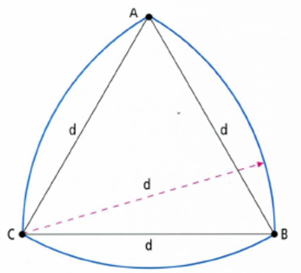
Полученная фигура называется треугольником РЁЛО и является кривой постоянной ширины. Если использовать вал подобной формы, он ничем не будет отличаться от круглого вала. При вращении треугольник Рёло всегда соприкасается с поверхностью земли и блока, поскольку он всегда вращается вокруг одной из вершин, а расстояние от неё до дуги окружности является постоянной величиной
Вершинами треугольника Рёло могут быть скругленными, и при этом он по-прежнему будет обладать постоянной шириной. Чтобы построить такой треугольник, достаточно продлить его стороны на произвольное расстояние, затем, зафиксировав центр окружности в одной из вершин, соединить концы продленных сторон дугами, как показано на рисунке:
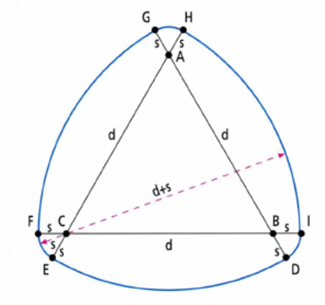
Все вышесказанное можно обобщить и для трех измерений, то есть можно построить геометрические тела постоянной ширины, подобные сфере. Простейшее из них можно получить вращением треугольника Рёло вокруг одной из его осей симметрии. Еще одно подобное тело можно получить, проведя аналогичные построения, но в пространстве: за основу берется пирамида, а не треугольник, и поверх ее граней строятся части сферы. Полученное тело будет вращаться в пространстве аналогично треугольнику на плоскости
Треуольник Рело: применение
Классические кинопроекторы всегда издают характерный стрекочущий звук. Он возникает из-за использования треугольников Рёло в механизме проектора. При показе фильма на экране на очень короткий промежуток времени (1/24 секунды) показывается кадр, после чего кинопленку необходимо провернуть, чтобы показать на экране следующий кадр. В этот момент затвор должен быть закрыт, чтобы на экране не было расплывчатого изображения. Получается, что движение ленты должно чередоваться с остановками. Это достигается путем равномерного вращения треугольника Рёло вокруг одной из его вершин. Треугольник Рёло находится внутри прямоугольной рамки, которая поднимается и опускается. Рамка остается неподвижной половину периода вращения треугольника, после чего перемещается в новое положение, где остается неподвижной такое же время. Затем весь цикл повторяется
Другое важное применение кривых постоянной ширины основано на возможности построения выпуклой кривой, внутри которой треугольник Рёло может перемещаться так чтобы все его вершины постоянно соприкасались с этой кривой. Благодаря этому свойству немецкий инженер Феликс Ванкель в 1924 году спроектировал роторный двигатель, в котором поршни были заменены ротором в форме треугольника Рёло. Ротор вращается внутри кривой необходимых размеров, точно подобранных для корректной работы четырехтактного двигателя внутреннего сгорания. Первый прототип под названием DKM был изготовлен в 1957 году, о результат оставлял желать лучшего из-за сильной вибрации на малой скорости, большого расхода масла и невысокого момента. Сейчас применяется уже третье поколение подобных двигателей (Rx-7), их объём доведен до 1 308 кубических сантиметров, мощность атмосферного двигателя при 8 200 оборотах в минуту составляет 227 лошадиных сил. Классический поршневой двигатель той же мощности будет иметь шесть цилиндров и объём более трех литров
Как сверлить квадратные отверстия?
Можно ли просверлить квадратное отверстие? Здравый смысл подсказывает, что нет, но на самом деле это возможно. В этом нам помогут кривые постоянной ширины. Представим себе окружность, вписанную в квадрат. При вращении она всегда касается всех его сторон, причем точки касания всегда располагаются на серединах сторон. При вращении треугольник Рёло нужных размеров также может постоянно касаться всех сторон квадрата, но в разных точках, так как его ширина постоянна. Каждая вершина треугольника опишет квадрат со скругленными углами. В начале ХХ века это свойство натолкнуло британского инженера Гарри Джеймса Уоттса на мысль о возможности сверления квадратных отверстий. Добавим, что этот же принцип позволяет сверлить отверстия форме любых многоугольников с четным числом сторон. В сверлильном станке Уоттса центр вращения треугольника Рёло не фиксирован. Описываемая замкнутая кривая выглядит как идеальный квадрат, но в действительности представляет собой более сложную кривую, образованную четырьмя дугами эллипса. Скругленные углы квадратного отверстия также являются дугами эллипса.
Интересный факт о кривых постоянной ширины
Кривые постоянной ширины обладают некоторыми примечательными свойствами. Рассмотрим, например, простой треугольник Рёло и вычислим его периметр. Он состоит из трёх равных круговых секторов с углом 60° и радиусом d, равным длине стороны треугольника. Так как 60° – это одна шестая от 360, длине дуги L для каждого сектора равна шестой части длины всей окружности C.
Иными словами:
L = 1/6 х C = 1/6 x 2пd = 1/3пd.
Общий периметр Р получается сложением длин дуг трех круговых секторов. Имеем:
Р=3 х (1/3 па) = пd
Это в точности совпадает с периметром окружности диаметра d, которая также является кривой постоянной ширины, равной d. Самым примечательным является тот факт, что это не случайное совпадение, а общий результат, одинаковый для всех подобных кривых. Можно показать, что все кривые равной постоянной ширины вне зависимости от формы имеют равный периметр.
Площадь этих кривых, даже если их ширина совпадает, изменяется в зависимости от формы фигуры. Однако треугольник Рёло занимает особое место. Его площадь, примерно равная 0,705d^2, что является минимально возможной.
Франц Рёло
Хотя кривые постоянной ширины были известны с древних времен, треугольники Рёло впервые изучил инженер и математик Франц Рёло (1829-1905), преподаватель Берлинской королевской технической академии. Он выполнил исследование всех механизмов, имевших большое значение в различные моменты истории. За огромный вклад в развитие математики, в 1912 году в Дании ему был установлен памятник.
Подготовка к ОГЭ по математике 2020 — задания 1 — 5 с подробными решениями.
