Подготовка к ОГЭ по математике: задание 23.2

Постройте график функции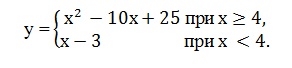                                                                                                                                                                                                                                                                                                            

Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.

Решение:

1. График заданной функции состоит из двух частей.  Областью определения данной функции является множество всех действительных чисел, так как в правых частях многочлены.
2. Рассмотрим  функцию y = x² -10x +25. После преобразования имеем: y = (x — 5)² . Это квадратичная функция, графиком которой является парабола. Ветви параболы направлены вверх. Вершина параболы точка с координатами (5;0)  ось симметрии x=5. Для построения графика возьмем точки большие или равные 4.
   

   x	4	5	6	7
   y	1	0	1	4

3. Вторая часть искомой функции имеет вид y = x — 3. Это линейная функция,  график  —  прямая. Для построения прямой возьмем 2 точки. X берем меньше 4.
   

   x	0	1
   y	-3	-2

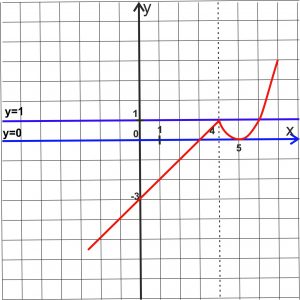
   Далее нужно отметить   точки на координатной плоскости и построить график функции, состоящий из двух частей.

4. По изображенному рисунку  легко определить, что прямая y = m  имеет с графиком ровно две общие точки когда y = 0 и y = 1. Поэтому, m = 0 и m = 1.   Ответ: 0; 1. Построение графика функции(задание 23.1)