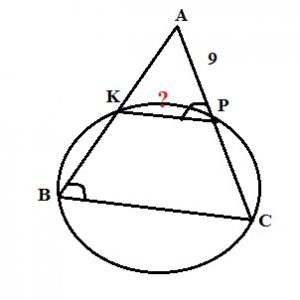
Окружность пересекает стороны AB и AC треугольника ABC в точках K и P соответственно и проходит через вершины B и C. Найдите длину отрезка KP, если AP=9, а сторона BC в 3 раза больше стороны AB.
Дано:
ᐃABC,
окружность пересекает
ᐃ в точках K и P,
AB = 3BC,
AP = 9.
Найти: KP.
Решение:
Пусть BC = x, тогда AB =3x.
Рассмотрим четырехугольник BKCP.
BKCP вписан в окружность, поэтому выполняется условие :
<B + <P = 180° и <K +<С = 180°.
Пусть <B = α, тогда <P =180° — α . <CPK = <P.
<APK + <CPK = 180°(смежные углы).
<APK = 180° — <CPK = 180° -(180° — α) = α.
ᐃ ABC подобен ᐃAPK по двум углам.
У них:
- <A — общий;
- <B = <APK = α.
По определению подобия имеем: PK : BC = AP : AB. Подставив известные значения в данную формулу и выражаем PK.
PK = 9x:3x = 3.
Ответ: PK = 3.
