Задание 25 (1) ОГЭ математика

Решаем задание 25.1 из второй части ОГЭ по математике. Это задание на доказательство  утверждения и  оценивается в 2 балла, если доказательство верное и все шаги в ходе доказательства обоснованно верные. Если же есть неточности в ходе доказательства, то оценка за задание составит 1 балл.

Задание 25 (1) ОГЭ математика

В выпуклом четырехугольнике ABCD  углы DAC и DBС равны. Докажите, что углы СDB  и CAB также равны.

Дано: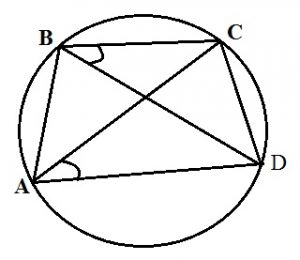 

ABCD — выпуклый четырехугольник,

<DAC = <DBС.

Доказать, что <СDB = <CAB.

Доказательство:

1. Так как четырехугольник ABCD выпуклый, то вокруг него можно описать окружность. Углы DAC и DBС вписанные и опираются на дугу СD,                <DAC = <DBС.
2. Углы СDB  и CAB являются вписанными в окружность, так как вершины углов лежат на окружности, а стороны пересекают окружность.
3. <СDB опирается на дугу BC  и  <CAB опирается на дугу BC.
4. Если углы, вписанные в окружность опираются на одну дугу, то они равны (свойство вписанных углов).
5. Поэтому, <СDB = <CAB. Что и  требовалось доказать.