Задание 12 ЕГЭ математика профиль( 20 вариант Ященко 2018)

Решаем 12 задание 20 варианта из сборника для подготовки к ЕГЭ по математике(профиль) автор Ященко И.В.

Найдите наибольшее значение функции y = 11 +24x -2x√x на отрезке [63; 65].

Решение:

Для нахождения наибольшего значения функции на отрезке [63; 65] нужно сравнить значения функции в точке экстремума и на концах отрезка. Данная функция непрерывна на отрезке [63; 65]. Найдем производную

y ‘ = 24 — 3√x.

Найдем критические точки функции, для этого приравняем производную к нулю и решим уравнение

 24 — 3√x = 0,

x = 64 — критическая точка функции.

На графике покажем знаки производной функции

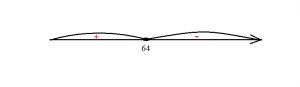
Точка x = 64 является точкой экстремума (максимум), так как в этой точке производная меняет знак с  +  на  — .

Точка 64 лежит на отрезке [63; 65] и на промежутке (-∞; 64]функция возрастает, а на промежутке [64;+∞) — убывает. Следовательно, наибольшего значения функция достигает в точке максимума.  Найдем наибольшее значение, применяя рациональные способы вычислений

y(64) = 11 + 24·64 -2·64·8 = 11 + (24·64 -16·64) = 11 + 64(24-16) = 11 + 64·8 = 11 + (60 +4)8 = 11 +60·8 + 4·8 = 11 + 480 + 32 = 523.

Ответ: 523 — наибольшее значение функции.