Задание 26 ОГЭ математика (324607)

Разбираем прототип задания 26 из второй части экзамена по математике в 9 классе(ОГЭ). Эта задача по геометрии взята из открытого банка задание огэ математика Федерального института педагогических измерений. Максимальный балл за решение этой задачи составляет 2 балла.

Задание 26 огэ математика (324607)

Найдите острые углы прямоугольного треугольника, если его гипотенуза равна 12,  а площадь равна 18.

Дано:       

ᐃABC – прямоугольный (<B = 90°),

AC =12,

S_ABC = 18.

__________________________

Найти: <A и <C.

Решение:

Сделаем дополнительное построение. Для этого из вершины B треугольника на гипотенузу опустим высоту BH и медиану BM.

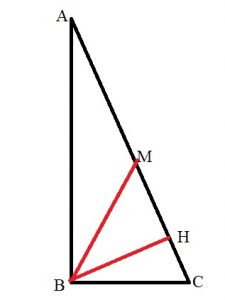
Воспользуемся формулой  площади прямоугольного треугольника, чтобы найти высоту BH.

S_ABC =( BH · AC):2,

( BH · 12):2 = 18,

BH = 3.

Медиана, проведенная гипотенузе равна половине гипотенузы: BM = AM = CM = 6.

Рассмотрим ᐃMBH – прямоугольный (<BHM = 90°).

BH = BM:2.

Следовательно, <HMB = 30°, этот угол является внешним углом для  ᐃMBА.

Внешний угол и внутренний угол при одной вершине являются смежными углами.

По свойству смежных углов можно записать равенство:

<HMB + <BMA = 180°,

<BMA = 180° — <HMB,

<BMA = 180° — 30° = 150°.

Так как ᐃMBА равнобедренный, то < MAB = <ABM = (180° — 150°):2 = 15°.

<A треугольника ABC найден и равен 15 градусам.

Найдем второй острый угол треугольника ABC, используя свойство острых углов прямоугольного треугольника.

<A + <С = 90°,

<С =90° — 15° = 75°.

Ответ: 15° и 75°.

Предлагаю ознакомиться с решением задания 24 ОГЭ математика, в котором тоже из вершины прямого угла  опущены высота и медиана на гипотенузу.