Разбираем прототип задания 26 из открытого банка заданий огэ математика Федерального института педагогический измерений.
Задание 26 огэ математика (324604)
В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 4. Найдите стороны треугольника ABC.
Дано: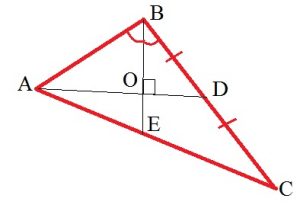 
ᐃABC,
BE — биссектриса,
AD — медиана,
BE ⊥ AD,
BE = AD=4.
________________
Найти: AB, BC, AC.
Решение:
Рассмотрим треугольники ABO и DBO.
У них:
BO — общая сторона,
<AOB = <DOB = 90° (BE — медиана),
<ABO = <DBO (AD — биссектриса).
Значит, треугольники равны по стороне и прилежащим углам.
Поэтому, AB = DB.
Через точку С проведем прямую параллельную AD. Продолжим сторону AB до пересечения с построенной прямой параллельно AD.
M — точка пересечения прямых.
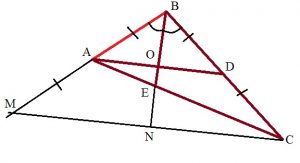
AD параллельна MC. В ᐃMBC (равнобедренный ) AВ является средней линией. AB = MC:2. MC = 8, MN = NC = 4.
BN и CA — медианы, пересекающиеся в точке E, которая их делит в отношении 2 к 1, начиная от вершины.
Поэтому, BE : EN = 2:1,
4: EN = 2:1,
EN = 2.
BN = BE + EN = 4 + 2 = 6.
Рассмотрим ᐃMBN — прямоугольный ( по свойству медиана равнобедренного треугольника, проведенная к основанию, является высотой). Далее находим MB, применив формулу прямоугольного треугольника — теорему Пифагора:
MB = 2√13.
MB = BC =2√13, AB = √13.
Итак, осталось найти третью сторону треугольника ABC — AC.
Для этого сначала из прямоугольного треугольника AOB найдем сторону BO? применив теорему Пифагора.
BO = 3.
EO = BE — BO = 4 — 3 = 1.
Аналогично находим AE из прямоугольного треугольника AOE.
AE = √5.
Медиана СA точкой пересечения медиан E делит ее в отношении:
CE : EA = 2 : 1,
CE : √5 = 2 : 1,
CE = 2√5.
AC = AE + CE = √5 + 2√5 = 3√5 .
Ответ: AB = √13, BC =2√13, AC =3√5 .
Правильно решив 26 задание ОГЭ математика можно получить максимально 2 балла. Но если есть вычислительная ошибка, либо пропущены существенные объяснения, то поставят 1 балл.
Вот еще одно задание из 2 части экзамена — 24 задание огэ вариант 165 .
