Решаем задание 26 огэ математика (вторая часть модуль Геометрия) вариант 165 с сайта Алекс Ларин.
Задание 26 огэ математика вариант 165 Алекс Ларин
В выпуклом равностороннем шестиугольнике ABCDЕF углы при вершинах А, С и Е –прямые. Найдите площадь шестиугольника, если его сторона равна
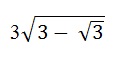
Дано: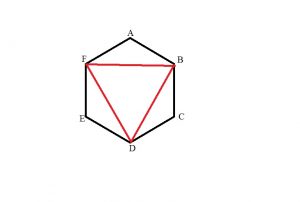 
ABCDЕF — равносторонний шестиугольник,
<A = <С = <E = 90°,
Найти площадь шестиугольника.
Решение:
Сделаем дополнительное построение. Проведем диагонали шестиугольника FB, BD, FD.
Так как шестиугольник ABCDЕF — равносторонний, то все его стороны равны.
ᐃABF = ᐃCDB = ᐃEFD ( по двум сторонам и углу между ними).
Равные треугольники имеют равные площади.
Найдем площадь одного треугольника.
По формуле площади прямоугольного треугольника, площадь прямоугольного треугольника равна половине произведения катетов.
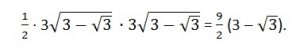
Рассмотрим треугольник FBD. Этот треугольник равносторонний. найдем сторону FB треугольника FBD из прямоугольного треугольника ABF по теореме Пифагора.
FB2 = AF2 + AB2,
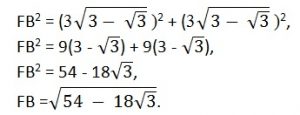
Найдем площадь ᐃFBD по формуле половина произведения сторон на синус угла между ними. Угол между сторонами равностороннего треугольника равен 60 градусам.
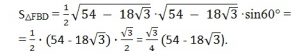
Найдем площадь шестиугольника, она складывается из площадей четырех треугольников.
S ABCDЕF = 3SᐃABF + SᐃFBD,
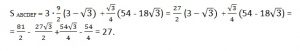
Ответ: 27.
Разбор варианта 165 Алекс Ларин огэ математика с подробным решением и ответами:
1 часть модуль Алгебра вариант 165 Алекс Ларин
1 часть модуль Геометрия вариант 165 Алекс Ларин
Задание 22 вторая часть модуль Алгебра вариант 165 Алекс Ларин
Задание 24 вторая часть модуль Геометрия вариант 165 Алекс Ларин
