Вариант 167 Алекс Ларин решение 1 часть Геометрия

Разбираем задания 15 -20 из 1 части модуля Геометрия тренировочный вариант 167 Алекс Ларин решение и ответы.

Вариант 167 Алекс Ларин решение 1 часть Геометрия

 

Задание 15 вариант 167 Алекс Ларин

Две трубы, диаметры которых равны 36 см и 48 см, требуется заменить одной, площадь поперечного сечения которой равна сумме площадей поперечных сечений двух данных. Каким должен быть диаметр новой трубы? Ответ дайте в сантиметрах.

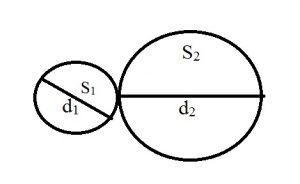
Обозначим d₁ и  d₂ диаметры окружностей 36 см и 48 см соответственно, тогда их площади  — S₁ и  S_{2 .}

Радиусы этих окружностей равны 18 см и 24 см.

Чтобы найти диаметр новой трубы нужно найти площади поперечного сечения каждой трубы и сложить.

Площадь поперечного сечения трубы  — это площадь круга, которая вычисляется по формуле S = πR².

S = S₁ + S_{2 .}

S₁ = π·18²= 324π

S₂ = π·24²= 576π

S₁ + S₂ =324π  +  576π = 900π

πR²= 900π

R²= 900

R = 30(см) — радиус новой трубы

Следовательно, диаметр новой трубы равен 60 см.

Ответ: 60 см.

Задание 16 вариант 167 Алекс Ларин

Окружность с центром в точке О описана около равнобедренного треугольника АВС, в котором АВ = ВС и <АВС = 138°. Найдите величину угла ВОС. Ответ дайте в градусах.

 

 

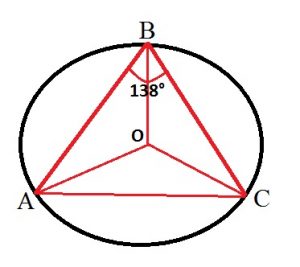
<АВС  — вписанный угол, он  равен половине соответствующего ему центрального угла AOC, то есть <AOC = 276°. 

Треугольники AOB и COB равны по трем сторонам. <AOB = <COB = (360° — 276°):2 = 42°.

Ответ: 42.

 

 

Задание 17 вариант 167 Алекс Ларин

В треугольнике ABC BM – медиана и BH – высота. Известно, что AC=97 и BC=BM. Найдите AH.

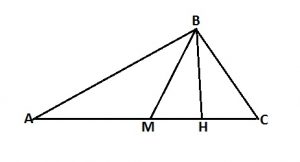
AM = CM = 97:2 = 48,5 (BM — медиана).

ᐃMBC — равнобедренный(BC=BM).

BH — высота равнобедренного треугольника, проведенная к основанию, она является медианой.

MH = HC = 48,5:2 = 24,25.

AH = AM + MH = 48,5 + 24,25 = 72,75.

Ответ: 78,75.

Задание 18 вариант 167 Алекс Ларин

В треугольнике со сторонами 15 и 3 проведены высоты к этим сторонам. Высота, проведённая к первой стороне, равна 1. Чему равна высота, проведённая ко
второй стороне?

Воспользуемся формулой площади треугольника — половина произведения высоты на основание.

Обозначим высоту, проведенную ко второй стороне — x.

Составляем уравнение

1/2·1·15 = 1/2·x·3;

x = 5.

Ответ: 5.

Задание 19 вариант 167 Алекс Ларин

Найдите угол ABC. Ответ дайте в градусах.

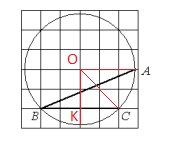
Угол ABC вписан в окружность и соответствует центральному углу AOC.

<AOC= <KOC:2 = 45°.

<ABC = <AOC:2 = 22,5°.

Ответ: 22,5.

 

 

 

Задание 20 вариант 167 Алекс Ларин

Какие из следующих утверждений верны?
1. Если в параллелограмме диагонали равны и перпендикулярны, то этот
параллелограмм — квадрат.
2. Площадь трапеции равна произведению средней линии на высоту.
3. Диагонали любого прямоугольника делят его на 4 равных треугольника.

Правильные утверждения только под номерами 1 и 2.

3 утверждение верно только когда фигура является квадратом.

Ответ: 12.

Ответы вариант 167 Алекс Ларин решение 1 часть Геометрия

задание	15	16	17	18	19	20
ответ	60	42	72,75	5	22,5	12

Вариант 167 Алекс Ларин 1 часть Алгебра

Вариант 166 Алекс Ларин  1 часть Геометрия