Вариант 221 Ларин решение 1- 8 задания (1 часть профиль)

Разбираем тренировочный вариант 221  задания 1-8  первой части ЕГЭ профильного уровня с сайта  Ларина.

Вариант 221 Ларин решение 1- 8 задания (1 часть профиль)

Задание 1 Вариант 221 Ларин 

Когда  Аристарх  Луков‐Арбалетов  сдал  ОГЭ,  друзья  подарили  ему  10  биткоинов. Сколько  раз  Аристарх  может  оплатить 6‐летнее  обучение  в  ВУЗе  ,  если  стоимость  обучения 300 тыс. рублей за год, к моменту оплаты курс биткоина был 17000 долларов  США, а один доллар стоил 57 рублей?

Узнаем сколько рублей составляют 10 биткоинов.

17000·10·57 = 9690000(руб)

За 6‐летнее  обучение  в  ВУЗе нужно заплатить 6·300000 = 1800000(руб)

Разделив 9690000 на 1800000 получаем 5, то есть оплатить обучение можно будет 5 раз.

Ответ: 5.

Задание 2 Вариант 221 Ларин 

20000 — 5000 = 15000

15000·57  = 855000(рублей)

Ответ: 855000.

Задание 3 Вариант 221 Ларин 

На  клетчатой  бумаге  (сторона  клетки  1  см)  изображён  четырёхугольник.  Найдите  его  площадь.  Ответ  выразите  в  квадратных сантиметрах.

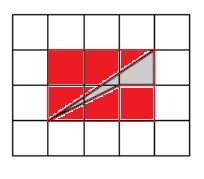
Достроим фигуру до прямоугольника.

Чтобы найти площадь искомого четырехугольника, нужно из площади прямоугольника вычесть площади двух прямоугольных треугольников и квадрата.

S = 3·2 — 0,5·3·2 — 0,5·1·2 — 1 = 6 — 3 — 1  — 1 = 1.

Ответ: 1.

 

Задание 4 Вариант 221 Ларин 

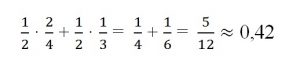
Ответ: 0,42.

Задание 5 Вариант 221 Ларин 

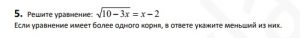
Сначала найдем область определения данного уравнения, решив систему из двух неравенств:

10 — 3x ≥ 0 и x- 2 ≥ 0. Итак, ОДЗ уравнения  2 ≤ x ≤ 3 1/3.

Далее, возводим обе части уравнения в квадрат и решаем квадратное уравнение по теореме, обратной теореме Виета.

10 — 3x = x² — 4x + 4;

x² — x — 6 = 0.

x₁ = -2 — не входит в область определения.

x₂ = 3

Ответ: 3.

Задание 6 Вариант 221 Ларин

Четырёхугольник  ABCD  вписан  в  окружность,  причём BC  =CD. Известно,  что  угол  ADC  равен  93°.  Найдите,  под каким  острым  углом  пересекаются  диагонали  этого четырёхугольника. Ответ дайте в градусах.

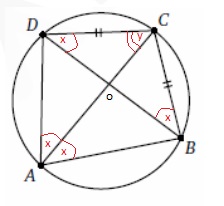
ᐃСDB — равнобедренный (DC = BC).

По свойству углов равнобедренного треугольника <CDB = <CBD .

Пусть <CDB = <CBD = x, <DCO = y.

<CBD = <ADC = x (вписанные углы, опирающиеся на одну дугу  DС).

Рассмотрим ᐃAOD и найдем сумму углов этого треугольника.

<AOD = 93° — x.

<AOD — внешний угол треугольника DCO, равен сумме внутренних не смежных с ним углов.

<AOD = x + y.

Cумма  углов  ᐃAOD:

x + 93° — x + x + y = 180°

x + y = 180° — 93°

x + y = 87°

<AOD = 87° — острый угол, под которым пересекаются диагонали четырехугольника.

Ответ: 87.

Задание 7 Вариант 221 Ларин

Прямая,  изображенная  на  рисунке,  является  графиком одной из первообразных функции  y = f(x). Найдите  f (2).

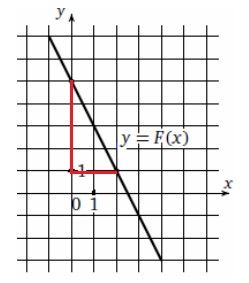
По определению первообразной имеем F'(x) = f(x), f(2) =  F'(2) .

Значение производной  — это тангенс угла наклона графика функции y = F(x) к положительной полуоси абсцисс.

Достраиваем прямоугольный треугольник и ищем

tgα = 4:2 = 2.

Так как угол наклона тупой, то f(2) = -2.

Ответ: -2.

 

 

Задание 8 Вариант 221 Ларин

В  правильной  треугольной  призме ABCA₁B₁C₁,  стороны  оснований  которой  равны  2,  боковые  ребра  равны  1, проведите  сечение  через  вершины ABC₁.  Найдите  его  площадь.

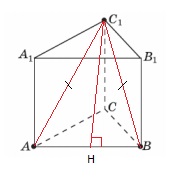
ᐃAA₁C₁   прямоугольный.

По тереме Пифагора найдем AC₁  

AC₁ = √5

ᐃAC₁B — равнобедренный( AC₁=C₁B = √5)

C₁H — высота и медиана.

AH = HB = 1.

C₁H = 2 ( по теореме Пифагора для треугольника AC₁H ).

S_ABC1=0,5 ·2·2 = 2.

Ответ:2.

Ответы вариант 221 Ларин  1- 8 задания (1 часть профиль)

задание	1	2	3	4	5	6	7	8
ответ	5	855000	1	0,42	3	87	-2	2

 

Задание 13 Вариант 221 ЕГЭ профиль Алекс Ларин