Разбираем тренировочный вариант 222 Ларин решение 1 — 6 заданий 1 части профильного ЕГЭ по математике.
Вариант 222 Ларин решение 1- 6 задания (1 часть профиль)
Задание 1 вариант 222 Ларин решение
Тетрадь стоит 24 рубля. Сколько рублей заплатил покупатель за 60 тетрадей, если при покупке больше 50 тетрадей магазин делает скидку 10% от стоимости всей покупки?
- 60⋅24 = 1440(руб) — стоимость покупки без скидки.
- 1440:10 = 144(руб) — скидка при покупке больше 50 тетрадей.
- 1440 -144 = 1296(руб) — стоимость 60 тетрадей с учетом скидки.
Ответ: 1296.
Задание 2 вариант 222 Ларин решение
По рисунку видно, что наименьшее значение температуры с 6 до 9 часов вечера составляет 26 градусов Цельсия.
Ответ: 26.
Задание 3 вариант 222 Ларин решение
Найдите периметр четырёхугольника ABCD с вершинами A(−7; −2), B(−7; 2), C(5; −3), D(5; −7).
Чтобы найти периметр четырехугольника, нужно найти длины сторон этой фигуры.
Длины сторон находим по формуле нахождения длины вектора по его координатам
|AB| = |CD| = 4
|BC| = |AD| = 13
P =4+4+13+13= 34
Ответ: 34.
Задание 4 вариант 222 Ларин решение
В одной корзине имеется 5 шаров, из которых 3 белых, 2 черных, а во второй 6 шаров -1 белый и 5 черных. Из каждой корзины вынимают по одному шару. Найдите вероятность того, что вынутые шары будут разного цвета. Ответ округлите до сотых
Пусть событие А — из первой корзины вынут белый шар — 3/5,
событие B-из первой корзины вынут черный шар — 2/5,
событие С — из второй корзины вынут белый шар — 1/6,
событие D-из второй корзины вынут черный шар — 5/6.
Найдем вероятность того, что вынутые шары разного цвета.
P = A⋅D+B⋅С = 17/30 ≈ 0,57.
Ответ: 0,57.
Задание 5 вариант 222 Ларин решение
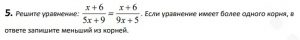
Одз уравнения: 5x+9≠0 и 9x+5≠0.
Используем основное свойство пропорции
(x +6)(9x +5) = (x +6)(5x + 9),
(x +6)(9x +5) — (x +6)(5x + 9) = 0,
(x +6)(9x +5 -5x — 9) = 0,
(x +6)(4x — 4) = 0.
x +6 = 0 или 4x — 4 = 0.
Корни уравнения: -6 и 1.
Меньший корень -6.
Ответ: -6.
Задание 6 вариант 222 Ларин решение
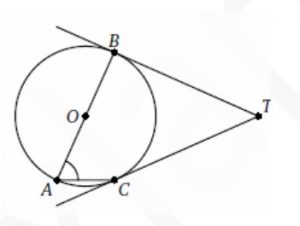
AB—диаметр окружности, TB и TC —касательные к ней. Найдите угол CTB, если < CAB=66°. Ответ дайте в градусах.
Сделаем дополнительные построения: проведем радиус OC и соединим точки С и T.
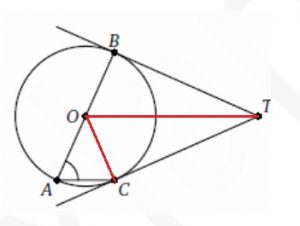Рассмотрим треугольник AOC. Это равнобедренный треугольник, так как AO = CO (радиусы).
<OAC = <OCA = 66°, <AOC=180° — 132° = 48°.
Треугольники COT и BOT равны по трем сторонам.
<TOC=<TOB= (180° — 48°):2 = 66°.
Треугольник OBT — прямоугольный, по свойству острых углов прямоугольного треугольника имеем: <BTO = 24°.
<CTB = 48°.
Ответ: 48.
