Высота прямоугольной трапеции в три раза больше меньшего основания, а большее основание равно 5. Найдите площадь трапеции, если её диагональ является биссектрисой угла при меньшем основании.
Дано: ABCD — прямоугольная трапеция, AB — высота трапеции, AB = 3BC, AD = 5, AC — биссектриса. Найти S трапеции.
Так как AC — биссектриса, то < ACB = < ACD.
У трапеции основания параллельны: BC ∥ AD.
< DAC = < ACB — как накрест лежащие при параллельных прямых и секущей AB.
△ADC — равнобедренный по признаку равнобедренного треугольник (два угла равны).
По определению равнобедренного треугольника CD = AD = 5.
Обозначим BC = x, AB = 3x.
Сделаем дополнительное построение — опустим высоту CM = 3x.
AM = BC = x, DM = 5 — x.
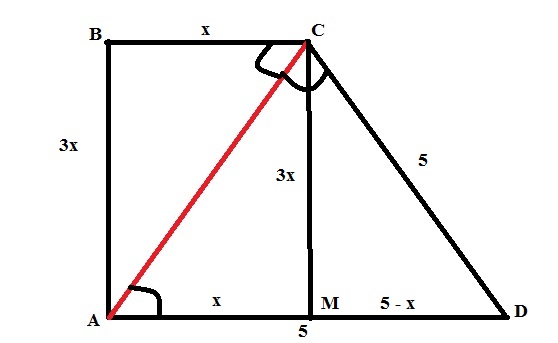
Рассмотрим △CDM — прямоугольный.
По теореме Пифагора имеем:
CD2 = CM2 + MD2,
52 = (3x)2 + (5 – x)2,
9x2 + 25 – 10x + x2 = 25,
10x2 – 10x = 0,
x(x – 1) = 0,
x = 0 или x = 1.
Итак, верхнее основание BC = 1, высота AB = 3.
Найдем площадь трапеции S по формуле: S = AB * (BC + AD) : 2.
S = 3 * (1 + 5) : 2 = 9.
Ответ: 9.
