Разбираем задания первой части перспективной модели измерительных материалов ОГЭ по математике. Модель опубликована на сайте ФИПИ 12 апреля 2019 года для общественно-профессионального обсуждения. Первая часть содержит 17 заданий с кратким ответом. Каждое задание оценивается в 1 балл. Задания 1 — 5 разобраны здесь.
Перспективная модель ОГЭ по математике 2020: разбор заданий
Решение:
Всего спортсменов 7 + 8 + 5 = 20 — все исходы.
Спортсмены из России — благоприятные исходы и их 7.
Находим вероятность, что первым будет выступать спортсмен из России.
7/20 = 35/100 = 0,35.
Ответ: 0,35.
Решение:
P = 220 ⋅ 220 /25 = 22 ⋅ 22⋅ 100/25 = 22⋅ 22 ⋅ 4 = 1936 (Вт).
Ответ: 1936.
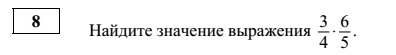
Применяем правило умножения обыкновенных дробей. Записываем произведение числителей и знаменателей. Сокращаем на 2 и имеем
(3 ⋅ 3) /( 2⋅ 5) = 9/10 = 0,9.
Ответ: 0,9.
Решение:
Используем теорему Виета.
Х1 + Х2 = — 3,
Х1 ⋅ Х2 = — 10.
Х1 = — 5, Х2 = 2.
Ответ: 2.
Решение:
Преобразовываем числовое выражение, используя свойства степеней.
5-7 ⋅ (55)2 = 5-7 ⋅ 510 = 5-7 + 10 = 53 = 125.
Ответ: 125.
Решение:
На первом рисунке изображен график квадратичной функции — парабола с ветвями, направленными вниз. Графику соответствует формула под А.
Второй рисунок — обратная пропорциональность (гипербола с ветвями во 2 и 4 координатных четвертях). (В)
3- ий рис. — линейная функция, график которой прямая. (Б)
Ответ: 132.
Решение:
Пусть а = 6,4. Проверяем утверждения.
- а — 4 = 6,4 — 4 = 2,4 > 0 (-).
- a — 6 = 6,4 — 6 = 0,4 > 0 (+).
- 6 — a = 6 — 6,4 = — 0,4 < 0 (-).
- 7 -a = 7 — 6,4 = 0,6 > 0 (+).
Ответ: 24.
Разбор заданий по геометрии
Решение:
Четырехугольник можно вписать в окружность, если выполняется условие:
<A + <C = <B + <D = 180°.
<A + <C = 180°.
82° + <C = 180°.
<C = 180° — 82° = 98°.
Ответ: 98.
Решение:
Sтр = (a + b)/2 ⋅ h, где a ивысота b — основания трапеции, а h — высота.
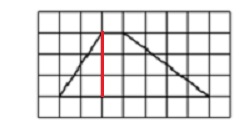Проведем высоту трапеции и подсчитаем по рисунку количество клеток, соответствующих данным отрезкам.
a = 1, b = 7, h = 3.
Sтр = (1 + 7)/2 ⋅ 3 = 4 ⋅ 3 = 12.
Ответ: 12.
Решение:
S = ah — формула площади параллелограмма.
Пусть высоты соответственно равны h1 и h2 .
S = ah1.
40 = 5h1.
h1= 40/5 = 8.
40 = 10h2.
h2= 40/10 = 4.
Ответ: 8.
Ответ: 13.
Перспективная модель ОГЭ по математике 2020: 17 задание
Решение:
Последовательность из количества приседаний, которое делала Вика каждый день в течение 15 дней образует арифметическую прогрессию.
Где первый член и сумма 15 членов соответственно равны: а1 = 30, S15 = 975.
Найдем сколько приседаний сделала Вика в пятнадцатый день — а15 .
Запишем формулу сумму пятнадцати членов арифметической прогрессии.
S15 = (a1 + а15)/2 ⋅ n, где n = 15.
975 = (30 + а15)/2 ⋅ 15.
а15= 100.
Найдем разность прогрессии d из формулы пятнадцатого члена арифметической прогрессии.
а15= a1 + d(n — 1).
100 = 30 + 14d.
d = 5.
Найдем сколько приседаний сделала Вика на пятый день.
а5= a1 + d(n — 1).
а5=30 + 5(5 — 1).
а5= 30 + 20 = 50.
Ответ: 5о.
Для решения геометрических задач первой и второй части перспективной модели измерительных материалов ОГЭ по математике 2020 необходимо повторить формулы прямоугольного треугольника .
