Решение 166 варианта Ларина 1 часть модуль Геометрия

Предлагаю разобрать решение 166 варианта Ларина. Решаем задания 15-20 из 1 части модуля Геометрия.

Решение 166 варианта Ларина 1 часть модуль Геометрия

Задание 15 вариант 166 Алекс Ларин

Составляем пропорцию и определяем пропорциональную зависимость.

В данной задаче обратная пропорциональная зависимость, так как при увеличении одной величины другая величина уменьшается.

Итак, 2: 5 = 1 :x.

За x обозначаем величину, обозначающую на сколько м опустится конец длинного плеча колодца  с «журавлём».

x = 2,5 (м)

Ответ: 2,5.

Задание 16 вариант 166 Алекс Ларин

В окружности с центром O отрезки AC и BD — диаметры. Центральный угол AOD равен 42°.  Найдите вписанный угол ACB.
Ответ дайте в градусах.

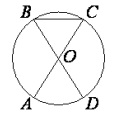
1. <AOD = <COB =42° ( как вертикальные углы);
2. <AOB=<COD = 180° — 42° = 138°(вертикальные, смежные);
3. угол ACB является вписанным углом в окружность и он равен половине дуги на которую опирается — дуга AB, то есть <ACB =138° :2 = 69°.

Ответ: 69.

 

 

 

 

Задание 17 вариант 166 Алекс Ларин

Основания трапеции равны 8 и 14. Найдите длину отрезка, соединяющего середины диагоналей трапеции.

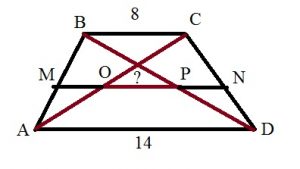
OP — отрезок, соединяющий середины диагоналей. Этот отрезок является частью средней линии MN.

MN = (8 + 14):2 = 11.

MN = MO + OP + PN.

MO = 8:2 = 4 (средняя линия треугольника ABC).

PN = 4 (средняя линия треугольника BCD).

OP = 11 -4 — 4 = 3.

Ответ:3.

Задание 18 вариант 166 Алекс Ларин

Площадь одной клетки равна 1. Найдите площадь фигуры, изображённой на рисунке.

1 способ.

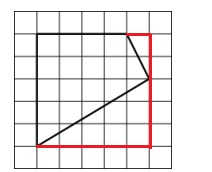
Достраиваем фигуру до квадрата.

Чтобы найти площадь искомой фигуры, нужно из площади квадрата вычесть площади достроенных треугольников.

Площадь прямоугольных треугольников находим по формулам.

S = 25 — (0,5·1·2 + 0,5·5·3) = 16,5.

 

2 способ. 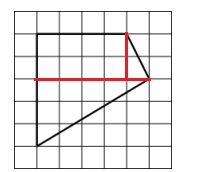                                                                                                                                                                                                                                                                                                 Разделяем фигуру по клеточкам на прямоугольник и 2 прямоугольных треугольника.

Площадь искомой фигуры будет состоять из площадей этих фигур.

S = 8 + 0,5 ·1·2 + 0,5·3 ·5 = 16,5.

 

 

Ответ: 16,5.

Задание 19 вариант 166 Алекс Ларин

В треугольнике ABC АВ = ВС = 13, AС = 10. Найдите tg A.

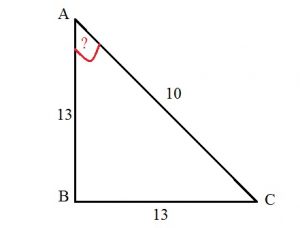
Мы знаем формулу, которая связывает тангенс с косинусом.

По теореме косинусов найдем косинус угла А.

cosA = 5/13.

1 + tg²A = 1/cos²A.

tgA = 2,4.

Ответ: 2,4.

 

Задание 20 вариант 166 Алекс Ларин

Правильные утверждения под номерами 2 и 3.

Ответ: 23.

Ответы 166 варианта Ларина 1 часть модуль Геометрия

 

Задание	15	16	17	18	19	20
Ответ	2,5	69	3	16,5	2,4	23

166 Вариант ОГЭ Алекс Ларин решение 1 части модуля Алгебра