Прямоугольный треугольник формулы

Треугольник называется прямоугольным, если у него один из углов является прямым. Стороны, прилежащие к прямому углу, называются катетами, а сторона, лежащая напротив прямого угла, гипотенузой.

Прямоугольный треугольник: основные формулы

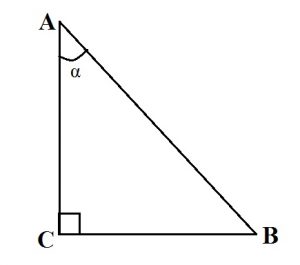
1. Пусть <A = 30°. Катет, лежащий напротив угла в 30 градусов, равен половине гипотенузы. CB = AB:2.
2. Сумма острых углов прямоугольного треугольника равна 90°. <A + <B = 90°.
3. Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов.  AB² = AC² + CB²

Прямоугольный треугольник:  формулы площади и проекции

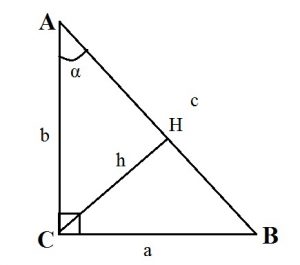
1. Высота прямоугольного треугольника, проведенная к гипотенузе, равна : h = (ab):c.
2. Высота прямоугольного треугольника, опущенная на гипотенузу, есть среднее пропорциональное между проекциями катетов на гипотенузу: CH² = AH·BH.
3. Катет прямоугольного треугольника — среднее пропорциональное или среднее геометрическое  между гипотенузой и проекцией этого катета на гипотенузу:  CA² = AB·AH;  CB² = AB·BH.
4. Медиана, проведенная к гипотенузе прямоугольного треугольника, равна ее половине.
5. Площадь прямоугольного треугольника равна половине произведения катетов. S = (ab):2.
6. Площадь прямоугольного треугольника равна половине произведения гипотенузы и высоты.  S = (hc):2.

Прямоугольный треугольник:  формулы тригонометрия

1. Косинус острого угла прямоугольного треугольника равен отношению прилежащего катета к гипотенузе.                 cosα  = AC: AB.
2. Синус острого угла прямоугольного треугольника равен отношению противолежащего катета к гипотенузе.           sinα = BC:AB.
3. Тангенс  острого угла прямоугольного треугольника равен отношению противолежащего катета к прилежащему.    tgα  = BC:AC.
4. Котангенс острого угла прямоугольного треугольника равен отношению прилежащего катета к противолежащему.    ctgα  = AC:BC.
5. Основное тригонометрическое тождество:  cos²α + sin²α = 1.
6. Теорема косинусов: b² = a² + c² – 2ac·cosα.
7. Теорема синусов: CB :sinA = AC : sinB = AB.

Прямоугольный треугольник:  формулы для описанной окружности

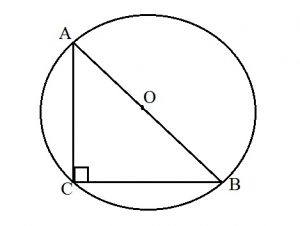
1. Радиус описанной окружности равен половине гипотенузы : R=AB:2.
2. Центр описанной окружности лежит на середине гипотенузы.

Прямоугольный треугольник:  формулы для вписанной  окружности

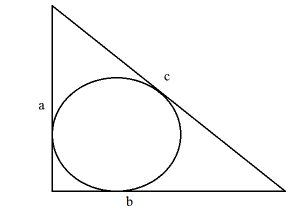
Радиус окружности, вписанной в прямоугольный треугольник, вычисляется по формуле: r = (a + b  -c):2.

Рассмотрим применение тригонометрических формул прямоугольного треугольника при решении задания 6(вариант 32) из  сборника для подготовки к ЕГЭ по математике профиль автора Ященко.

В треугольнике ABC угол С равен 90°, sinA = 11/14, AC =10√3. Найти АВ.

Решение:

1. Применяя основное тригонометрическое тождество, найдем cosA = 5√3/14.
2. По определению косинуса острого угла прямоугольного треугольника имеем: cosA = AC : AB, AB = AC : cosA = 10√3·14:5√3 = 28.

Ответ: AB = 28.

ЗАДАНИЕ 12 ЕГЭ МАТЕМАТИКА ПРОФИЛЬ( 20 ВАРИАНТ ЯЩЕНКО 2018)