Формулы сокращенного умножения

Тема «Формулы сокращенного умножения» изучается в школьном курсе математики в 7 классе. Для чего нужны формулы сокращенного умножения:

1. для рациональных преобразований выражений;
2. для нахождения квадратов больших чисел без калькулятора.

Формулы сокращенного умножения

1. разность квадратов двух выражений (a -b)(a +b) = a² – b²
2. квадрат суммы двух выражений  (a + b)² = a² + 2ab + b²
3. квадрат разности двух выражений (a — b)² = a² — 2ab + b²
4. куб суммы двух выражений  (a + b)³ = a³ + 3a²b + 3ab² +b³
5. куб разности двух выражений  (a — b)³ = a³ — 3a²b + 3ab² — b³
6. сумма кубов двух выражений  a³ + b³ = (a + b)(a² – ab + b²)
7. разность кубов двух выражений  a³ — b³ = (a — b)(a² + ab + b²)

Примеры применения формул сокращенного умножения

1. Задание 9 (25 вариант) из сборника для подготовки к ЕГЭ по математике профиль 2018  автор Ященко:                     Найдите значение выражения (√3 — √8)(√3 + √ 8) = (√3)² – (√ 8)² = 3 -8 = -5. В этом задании мы использовали формулу сокращенного умножения — разность квадратов двух выражений.
2. Задание 9(24 вариант) из сборника для подготовки к ЕГЭ по математике профиль 2018 автор Ященко:
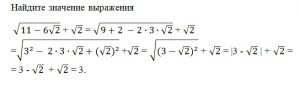
   В этом задании использовалась формула сокращенного умножения — квадрат разности двух выражений.
3.  Найти значение выражения  98² . Если находить это произведение в столбик, то это нерационально. Можно найти произведение, используя формулу сокращенного умножения — квадрат разности двух выражений. Для этого представим число 98 в виде разности чисел 100 и 2, а затем применим формулу.                                                                                                                                                              98² = (100 – 2)² = 100² — 2·100·2 + 2² = 10 000  — 400 +4 = 9604.

Пример  с решением  задания 12 ЕГЭ по математике профильного уровня