Готовимся к ОГЭ по математике, решаем задание 23 на построение графика функции с модулем. За это задание на экзамене можно получить максимум 2 балла.
Постройте график функции y= |x2 + 4x + 3|. Какое наибольшее число общих точек график данной функции может иметь с прямой параллельной оси абсцисс?
Решение:
Чтобы построить график функции y= |x2 + 4x + 3|, нужно сначала построить график функции y= x2 + 4x + 3. Это квадратичная функция, график которой парабола с ветвями направленными вверх. Выделим квадрат двучлена чтобы найти вершину параболы: x2 + 4x + 3 = (x2+ 4x + 4) — 1 = (x + 2)2-1. Мы преобразовали функцию y = (x + 2)2— 1. Вершина параболы имеет координаты (-2;-1) и ось симметрию x = -2. Построим параболу по точкам. В таблице приведены значения для правой ветви. Левая ветвь строится симметрично.
|
x |
-2 | -1 | 0 | 1 |
| y | -1 | 0 | 3 |
8 |
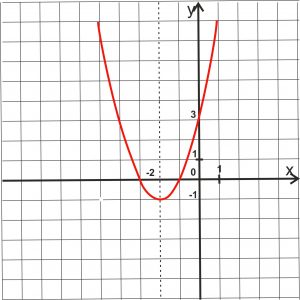
Далее часть графика над осью абсцисс сохраняем без изменений, а часть параболы, расположенную ниже оси абсцисс зеркально отображаем относительно оси OX. Рисунок к заданию находится в конце решения.
Первая часть задания 23 из ОГЭ по математике выполнена, т.е. построен график квадратичной функции под модулем. Осталось определить — какое наибольшее число общих точек график данной функции может иметь с прямой параллельной OX:
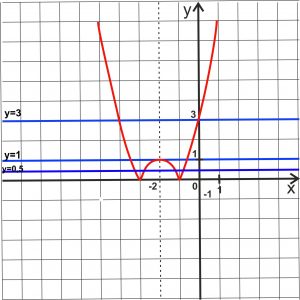
- если проведем прямую y=0, то получаем 2 общие точки;
- если значения y находятся в промежутке (0;1), то 4 общие точки;
- если проведем прямую y =1, то мы видим 3 общие точки;
- если y>1, то 2 точки.
Ответ: наибольшее число общих точек графика функции с прямой, параллельной оси абсцисс 4.
Посмотрите как решается еще одно задание 23 ОГЭ математика с модулем
