Продолжаем решать тренировочный вариант 221 Ларин. Разбираем 2 часть профильного уровня с 9 по 12 задание.
Задания с 1 по 8 тренировочного варианта 221 Алекс Ларин разобраны здесь.
Вариант 221 Ларин решение 9- 12 задания (2 часть профиль)
Задание 9 вариант 221 Ларин
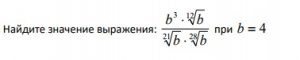
Преобразуем корни в степени и при нахождении значения выражения воспользуемся свойствами степеней, чтобы упростить его.

Ответ: 64.
Задание 10 вариант 221 Ларин

Пусть у = 9 + 1 = 10(м) — высота камня над землей.
Подставим все значения в искомую формулу и найдем x.
1/25x2 + 7/5x — 10 = 0,
Умножим обе части уравнения на 25.
x2 + 35x — 350 = 0,
По теореме, обратной теореме Виета находим два корня уравнения: 25 и 10.
Итак, максимальное расстояние, на которое нужно расположить машину равно 25 м.
Ответ: 25 м.
Задание 11 вариант 221 Ларин
Из городов A и B навстречу друг другу одновременно выехали с постоянными скоростями два автомобиля. Скорость первого автомобиля была в два раза больше скорости второго. Второй автомобиль прибыл в A на 1 час позже, чем первый прибыл в B. На сколько минут раньше произошла бы встреча автомобилей, если бы второй автомобиль ехал с той же скоростью, что и первый?
Обозначим расстояние между городами за 1.
x км/ч — скорость второго автомобиля,
2x км/ч — скорость первого автомобиля.
1/x ч — время второго автомобиля, 1/2x ч — первого.
Второй автомобиль прибыл в пункт В на час позже.
Составим уравнение
1/x — 1/2x = 1,
x = 0,5(км/ч) — скорость второго автомобиля.
2x = 1(км/ч) — скорость первого автомобиля.
Найдем время, через которое произошла бы встреча автомобилей, если бы они ехали с первоначальной скоростью.
t = 1/(x +2x) = 1/1,5 = 2/3.
Найдем время, через которое произошла бы встреча, если бы второй автомобиль ехал с той же скоростью, что и первый.
t = 1/(2x + 2x) = 1/2 .
Найдем на сколько минут раньше произошла бы встреча автомобилей
2/3 — 1/3 = 1/6(ч)
1/6 часа = 10 мин.
Ответ: 10.
Задание 12 вариант 221 Ларин

Область определения функции — все значения x кроме 0.
Выясним как ведет себя функция на отрезке[3,9].
Найдем производную функцию и,преобразовав ее, получим:
y’ =x2 — 36.
Приравняем производную к нулю и найдем критические точки: 6 и -6.
На отрезке от 3 до 6 производная меньше 0, функция убывает.
На отрезке от 6 до 9 производная больше 0, функция возрастает.
Точка 6 — точка минимума функции.
Наименьшее значение на [3,9] достигает функция в точке x = 6 и равно:
y(6) = (36-36+36)/6 = 6.
Ответ: 6.

2 Комментариев
Комментирование закрыто.